7 класс

СПРАВОЧНИК   ПО ГЕОМЕТРИИ, 7 КЛАСС

1. Геометрия  (греч. слова geо – «Земля» и metreo – «измеряю») – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).

2. В планиметрии (лат.слово planum – «плоскость» и metreo – «измеряю») изучаются свойства фигур на плоскости. В стереометрии ( греч. слова stereos – «объемный» и metreo – «измеряю») изучаются свойства фигур в пространстве.

       К основным геометрическим фигурам на плоскости относятся точка, прямая  линия (линия - лат. слово linea – «лен», «нить», «шнур», «веревка»).

      Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.

       Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение.

Точка обозначается заглавной (большой) латинской буквой, несколько точек разными буквами, чтобы их можно было различать.

Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.

      Прямую линию, или прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна.

        Прямая линия — это линия,  которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны. Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны.

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой.                                                                                                                

Прямая линия изображается так:

                                             а                                                                                

или

       Через любые две точки можно провести прямую, и притом только одну.

3.  Отрезок, луч, ломаная линия — простейшие геометрические фигуры на плоскости.

     Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком. Эти точки называются концами отрезка.

    Отрезок изображается так:  ЕМ, АВ. 

   Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:     А В

    Если на прямой вы поставили точку, то этой точкой прямая разбивается на два луча, противоположно направленных. Такие лучи называются дополнительными.

     В                  А                      С

        АВ и АС – дополнительные лучи.

     Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.

На рисунке  изображена трехзвенная ломаная линия.

   4. Угол  (лат.слово angulus – «угол») — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла. Или  угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.

   Если плоскость круга разделить на 360 равных частей радиусами, то 1/360 часть круга — это угловой градус (лат. слово gradus – «шаг», «ступень»), который обозначается знаком « ° » (читается — «градус»).  Следовательно, 1° = 1/360 часть круга.

          Круг составит 1/360 * 360 = 1° * 360 = 360°.

         Угол, равный плоскости круга, составляет 360° и называется полным углом.

5. Угол называется развёрнутым, если обе его стороны лежат на одной прямой.                   Развёрнутый угол равен 180°.

      Если плоскость круга разделить диаметром (двумя радиусами, расположенными на одной прямой линии) на две равные части, то плоскость полукруга составит  угол в   360°: 2 = 180°.

      Если плоскость круга разделить двумя диаметрами (горизонтальной и вертикальной линиями) на четыре равные части, то плоскость одной части составит угол в   360° : 4 = 90°.

6. Угол называется прямым, если он равен 90°, он равен четвертой части круга

7. Две геометрические фигуры называются равными, если их можно совместить наложением.

   Углы равны, если равны их градусные меры или у них при наложении одного угла на другой совпадают вершины и соответствующие стороны углов.

   8. Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).

Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.

9. Угол называется тупым, если он больше 90°, но меньше 180° (т.е. больше прямого, но меньше развёрнутого).

                       Угол 135°

 10. Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.

АС = ВС =1/2 АВ

11.  Биссектрисой (от лат. bi - "двойное", и sectio - "разрезание") угла называется луч, который исходит из вершины угла и делит  угол на две равные части (пополам)

12. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.

                ∠ АОВ + ∠ ВОС = 180° .

13. Два угла называются вертикальными (лат. слово verticalis – «вершинный»), если стороны одного угла являются продолжениями сторон другого.  Вертикальные углы равны.

 ∠АОВ=∠COD,     ∠ АОС = ∠ ВOD.

14. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла (перпендикуляр - лат. perpendicularis «отвесный»).

   Если прямые  AС и ВD  пересекаются  и ∠1 = ∠2= ∠3= ∠4 = 90°, то AС ⊥ ВD.

или

     Две прямые, пересекающиеся под прямым углом, называются перпендикулярными.

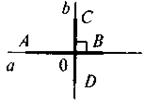
 Если прямая а и прямая в пересекаются в точке О и ∠СОВ = 90°, то а ⊥ в.

     Перпендикулярность прямых (или их отрезков) обозначают знаком перпендикулярности «⊥».

  Свойства перпендикулярных прямых

а) Через точку А можно провести только одну перпендикулярную прямую АH к прямой BT; остальные прямые, проходящие через точку А и пересекающие BT, называются наклонными   (прямые АB, AC и АT).

б) Длина перпендикуляра (длина отрезка АH), проведенного из точки А на прямую BT,— это самое короткое расстояние от A до BT.

              Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.

с) Несколько перпендикуляров, проведенных через различные точки к одной  прямой, никогда между собой не пересекаются.