Самостоятельные работы

 

Самостоятельная работа

«Аксиомы стереометрии и их следствия»

1 вариант

1.   Даны четыре точки, из которых три лежат на одной прямой. Верно ли утверждение, что все четыре точки лежат в одной плоскости? Ответ обоснуйте.

2.   а)   Докажите, что все вершины четырёхугольника ABCD лежат в одной плоскости, если его диагонали АС и BD пересекаются. б)   Вычислите площадь четырёхугольника, если его диагонали АС и BD  взаимно перпендикулярны, АС = 10  см,  BD = 12 см.

2 вариант

1.   Даны две пересекающиеся прямые. Верно ли утверждение, что все прямые, пересекающие данные, лежат в одной плоскости? Ответ обоснуйте.

2.   а)   Дан прямоугольник ABCD, О – точка пересечения его диагоналей. Известно, что точки А, В и О лежат в плоскости α. Докажите, что точки С и D также лежат в плоскости α  б)   Вычислите площадь прямоугольника, если АС = 8 см, < АОВ = 60⁰.

 

Самостоятельная работа 10кл

По геометрии урок 5

1. Пользуясь рис. , назовите а) четыре точки , лежащие в плоскости SАВ б) плоскость в которой лежит прямая MN , в) прямую , по которой пересекаются плоскости SАС и SВС.

2. Точка С – общая точка плоскости       и        .    Верно ли , что плоскости         и        пересекаются по прямой  с .  Ответ объясните  .

3. Через прямую  а   и  точку  А  можно провести  две различные плоскости . Каково взаимное расположение  прямой   а  и  точки  А . Ответ объясните .

4.  Плоскости         и          имеют три общие токи . Верно ли , что эти плоскости  совпадают .Ответ объясните .

5. Через А,  В  и С можно провести две различные плоскости . Каково  взаимное расположение  точек А , В  и С  . Ответ объясните.

6. Прямые А, В и С  имеют общую точку . Верно ли что данные прямые  лежат в одной плоскости . Ответ объясните.

7. Прямые а , в  и с попарно пересекаются . Верно ли , что данные прямые лежат в одной плоскости . Ответ объясните.

 

Следствия из аксиом стереометрии

Вариант 1

1. В плоскости двух пересекающихся прямых a и b задана точка C, не принадлежащая этим прямым. Прямая c, лежащая в данной плоскости, проходит через точку C. Как может быть расположена прямая c относительно данных прямых?

2. Даны три точки, не принадлежащие одной прямой. Докажите, что все прямые, пересекающие два из трех отрезков, соединяющих данные точки, лежат в одной плоскости.

3. Плоскость задана прямой c и не принадлежащей ей точкой C. Постройте в этой плоскости прямую a, отличную от данной прямой и не проходящую через данную точку.

4. Плоскость задана двумя пересекающимися в точке O прямыми a и b. Нарисуйте прямую c, которая пересекает данные прямые и не лежит в данной плоскости.

 

Вариант 2

1. Прямая d, лежащая в плоскости треугольника ABC, пересекает его сторону AB. Каким может быть взаимное расположение прямых d и BC?

2. В плоскости  проведены две параллельные прямые a и b. Докажите, что все прямые, пересекающие данные прямые, лежат в одной плоскости.

3. Плоскость задана двумя пересекающимися в точке O прямыми m и n. Постройте в этой плоскости прямую k, отличную от данных прямых и не проходящую через точку O.

4. Плоскость задана тремя точками D, E, F, не принадлежащими одной прямой. Нарисуйте прямую a, которая пересекает стороны DE и DF треугольника DEF и не лежит в данной плоскости.

 

Параллельность прямых в пространстве

Вариант 1

1. Запишите в правильной 4-угольнойой пирамиде SABCD все пары параллельных ребер.

2. В плоскости двух параллельных прямых a и b дана точка C, не принадлежащая этим прямым. Через точку C проведена прямая c. Как может быть расположена прямая c относительно прямых a и b.

3. Через точку, не принадлежащую данной прямой, проведите прямую, параллельную данной.

4. Найдите геометрическое место прямых, пересекающих две данные параллельные прямые.

Вариант 2

1. Запишите четыре пары параллельных ребер куба A…D₁.

2. Даны три прямые a, b и с. Как могут располагаться эти прямые, чтобы можно было провести плоскость, содержащую все данные прямые.

3. Даны две параллельные прямые a и b. Докажите, что любая плоскость, пересекающая одну из них, пересечет и другую.

4. Найдите геометрическое место прямых, параллельных данной прямой и пересекающих другую прямую, пересекающуюся с первой.

 

Параллельность прямой и плоскости

Вариант 1

1. Запишите ребра, параллельные плоскости грани CC₁D₁D правильной призмы ABCDEFA₁B₁C₁D₁E₁F₁.

2. Прямая a параллельна плоскости a; прямая b пересекает плоскость a в точке B; прямая c, пересекающая прямые a и b соответственно в точках E и F, пересекает плоскость a в точке C. Сделайте рисунок. Как могут располагаться относительно друг друга прямые a и b?

3. Плоскости a и b пересекаются по прямой c. Точка A принадлежит плоскости a, точка B – плоскости b. Постройте: а) прямую a, лежащую в плоскости a, проходящую через точку A и параллельную плоскости b; б) прямую b, лежащую в плоскости b, проходящую через точку B и параллельную плоскости a. Как будут располагаться относительно друг друга прямые a и b?

4. Точки A и B принадлежат смежным боковым граням пирамиды. Проведите в этих гранях через данные точки два отрезка, параллельные между собой.

Вариант 2

1. Запишите плоскости граней, параллельных ребру CC₁ параллелепипеда A…D₁.

2. Прямая a параллельна плоскости a; прямые b и c, пересекающие прямую a соответственно в точках B и C, пересекают плоскость a соответственно в точках D и E. Сделайте рисунок. Как могут располагаться относительно друг друга прямые a и b?

3. Плоскости a и b пересекаются по прямой c. Прямая a лежит в плоскости a. Докажите, что если: а) a пересекает плоскость b в точке A, то A принадлежит прямой c; б) a параллельна плоскости b, то она параллельна прямой c.

4. Точки A и B принадлежат смежным боковым граням призмы. Проведите в этих гранях через данные точки два отрезка, параллельные между собой.

 

Самостоятельная работа

«Параллельность прямых,  прямой и плоскости»

1 вариант

Дан треугольник АВС, Е є АВ, К є ВС,  ВЕ : ВА = ВК : ВС = 2 : 5.  Через прямую АС проходит плоскость α, не  совпадающая  с плоскостью треугольника АВС.

а)   Докажите, что ЕК || α.  б)   Найдите длину отрезка АС, если ЕК = 4  см

2 вариант

Дан треугольник АВС, М є АВ, К є ВС, ВМ : МА = 3 : 4. Через  прямую МК проходит плоскость α, параллельная прямой  АС.

а)   Докажите, что ВС : ВК = 7 : 3. б)   Найдите длину отрезка МК, если АС = 14  см.

 

Параллельность двух плоскостей

Вариант 1

1. Запишите параллельные плоскости параллелепипеда A…D₁.

2. Верны ли утверждения:

1) Через точку, не принадлежащую данной плоскости, проходит единственная плоскость, параллельная данной.

2) Если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.

3) Существует бесконечно много прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.

4) Если одна из двух данных плоскостей параллельна двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.

3. Докажите, что две плоскости, параллельные одной и той же третьей плоскости, параллельны между собой.

4. Отрезки AB и CD лежат соответственно в параллельных плоскостях a и b (рис. 2). Как могут располагаться относительно друг друга прямые AC и BD? Могут ли они быть параллельными?

Вариант 2

1. В треугольной пирамиде SABC проведите плоскость, параллельную ее основанию ABC.

2. Верны ли утверждения:

1) Если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.

2) Если плоскость пересекает две данные плоскости по параллельным прямым, то эти плоскости параллельны.

3) Существует бесконечно много плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.

4) Если две плоскости параллельны одной и той же прямой, то они параллельны.

3. Докажите, что если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую.

4. Отрезки AB и CD лежат соответственно в параллельных плоскостях a и b (рис. 3). Как могут располагаться относительно друг друга прямые AD и BC? Могут ли они пересекаться?

 

Самостоятельная работа

«Перпендикулярность прямой и плоскости»

1 вариант

1.   Прямая АВ перпендикулярна плоскости α, М и К – произвольные точки плоскости α. Докажите, что АВ перпендикулярна прямой МК.

2.   Треугольник АВС правильный, точка О – его центр. Прямая ОМ перпендикулярна к плоскости АВС.

а)   Докажите, что МА = МВ = МС. б)   Найдите МА, если АВ = 6 см, МО = 2 см.

2 вариант

1.   Прямая  МА перпендикулярна к плоскости треугольника АВС. Докажите, что МА  перпендикулярна прямой ВС.

2.   Четырёхугольник АВСD – квадрат, точка О – его центр. Прямая  ОМ перпендикулярна к плоскости квадрата.

а)   Докажите, что МА = МВ = МС = MD. б)   Найдите МА, если АВ = 4 см, ОМ = 1 см

 

Скрещивающиеся прямые

Вариант 1

1. В кубе A…D₁ запишите ребра, скрещивающиеся с ребром AB.

2. Запишите пары скрещивающихся ребер 4-угольной пирамиды SABCD.

3. Как расположены относительно друг друга прямые a и b на рисунке 1? Ответ обоснуйте.

4. Даны две скрещивающиеся прямые a и b и не принадлежащая им точка C. Постройте прямую c, проходящую через точку C и пересекающую прямые a и b.

Вариант 2

1. Запишите ребра, скрещивающиеся с ребром SA правильной 4-угольной пирамиды SABCD.

2. Запишите ребра, скрещивающиеся с диагональю B₁D куба A…D₁.

3. Плоскости a и b пересекаются по прямой c (рис. 1). Прямая a лежит в плоскости a и пересекает прямую c. Можно ли в плоскости b провести прямую, параллельную прямой a? Ответ обоснуйте.

4. Существуют ли две параллельные прямые, каждая из которых пересекает две данные скрещивающиеся прямые? Ответ обоснуйте.

 

Самостоятельная работа 10кл

По геометрии урок 12 Угол между плоскостями

1 вариант

1. Ребро  CD тетраэдра ABCD перпендикулярно плоскости АВС, АВ = ВС =АС =6, BD = 37. Найти двугранный угол DABC.

2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ сторона основания АВ = 6 см,  высота АА₁ = 9 см, а диагональ А₁С = 15см. Найти угол между диагональной плоскостью АСС₁А₁ и боковой гранью А₁В₁ВА.

3. Основанием прямой треугольной призмы АВСА₁В₁С₁ является равнобедренный треугольник АВС, в котором АВ = ВС = 20,

АС = 32. Боковое ребро призмы равно 24. Точка Р принадлежит ребру ВВ₁, причем ВР:РВ₁ = 1:3. Найти тангенс угла между плоскостями А₁В₁С₁ и АСР.

2. Вариант

1. Ребро  CD тетраэдра ABCD перпендикулярно плоскости АВС, АВ = ВС =АС =6, BD = 37. Найти двугранный угол BDCA.

2. Через центр О квадрата ABCD проведен перпендикуляр OF к плоскости квадрата. Вычислите угол между плоскостями BCF и ABCD, если FB = 5 дм, ВС = 6 дм.

3. Основание прямой треугольной призмы АВСА₁В₁С₁ - треугольник АВС, в котором АВ = ВС = 8, а один из углов равен 60°. На ребре АА₁ отмечена точка Р так, что

АР:РА₁ = 2:1. Найти тангенс угла между плоскостями АВС и СВР, если расстояние между прямыми АВ и С₁В₁ равно 183. 

Перпендикулярность прямой и плоскости

Вариант 1

1. Докажите, что прямая, перпендикулярная плоскости, пересекает эту плоскость.

2. Через центр O квадрата ABCD проведена прямая OK, перпендикулярная плоскости этого квадрата. Докажите, что прямая AK перпендикулярна прямой BD.

3. Найдите геометрическое место точек, принадлежащих прямым, проходящим через данную точку и перпендикулярным данной прямой.

4. Точка M принадлежит боковой грани ABD треугольной пирамиды ABCD, у которой AB = BD и AC = CD. Постройте сечение этой пирамиды плоскостью, проходящей через точку M и перпендикулярной прямой AD.

Вариант 2

1. Прямая a, перпендикулярная плоскости a, пересекает эту плоскость в точке A. Докажите, что прямая b, проходящая через точку A и перпендикулярная прямой a, лежит в плоскости a.

2. Через точку M – середину стороны AB равностороннего треугольника ABC проведена прямая MH, перпендикулярная плоскости этого треугольника. Докажите перпендикулярность прямых AB и HC.

3. Даны прямая a и не принадлежащая ей точка A. Найдите геометрическое место прямых, проходящих через точку A и перпендикулярных прямой a.

4. В прямоугольном параллелепипеде A…D₁ постройте сечение, проходящее через точку K, внутреннюю точку диагонального сечения AA₁C₁C, и перпендикулярное прямой BB₁.

 

Перпендикуляр и наклонная 

Вариант 1

1. Дана плоскость a. Из точки A проведены к ней две наклонные AB = 20 см и AC = 15 см. Проекция первой наклонной на эту плоскость равна 16 см. Найдите проекцию второй наклонной.

2. Из точки M, не принадлежащей плоскости g, проведены к ней равные наклонные MA, MB и MC. Докажите, что основания наклонных принадлежат одной окружности. Найдите ее центр.

3. Из точки B проведены к плоскости b две равные по 2 см наклонные. Угол между ними равен 60⁰, а между их проекциями – 90⁰. Найдите перпендикуляр, опущенный из точки B на плоскость b.

4. Дан треугольник со сторонами 13 см, 14 см и 15 см. Точка M, не принадлежащая плоскости этого треугольника, удалена от сторон треугольника на 5 см. Найдите перпендикуляр, опущенный из точки M на плоскость данного треугольника.

Вариант 2

1. Из точки A проведены к плоскости a наклонная AB = 9 см и перпендикуляр AO = 6 см. Найдите проекцию этого перпендикуляра на данную наклонную.

2. Найдите геометрическое место точек в пространстве, равноудаленных от всех точек данной окружности.

3. Из данной точки проведены к данной плоскости две равные наклонные, образующие между собой угол 60⁰. Угол между их проекциями – прямой. Найдите угол между каждой наклонной и ее проекцией.

4. Точка M удалена от каждой вершины правильного треугольника на 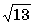см, а от каждой его стороны – на 2 см. Найдите перпендикуляр, опущенный из точки M на плоскость треугольника.

Угол между прямой и плоскостью

Вариант 1

1. В пирамиде боковые ребра одинаково наклонены к плоскости основания. В какую точку проектируется вершина пирамиды?

2. В кубе A…D₁ найдите косинус угла между ребром AA₁ и плоскостью AB₁D₁.

3. К плоскости a проведена наклонная MH (H принадлежит плоскости a). Докажите, что если проекция наклонной