Решение задач по готовым чертежам

Таблица 8.13. Декартовы координаты на плоскости

 

 

Таблица 8.14. Симметрия относительно точки

 

Таблица 8.15. Симметрия относительно прямой

 

 

 

 

 

 

Таблица 8.16. Векторы на плоскости

 

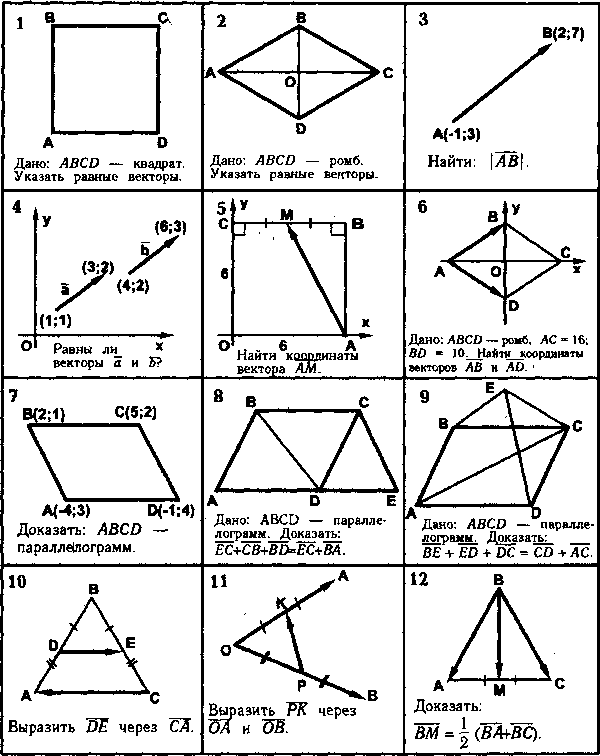
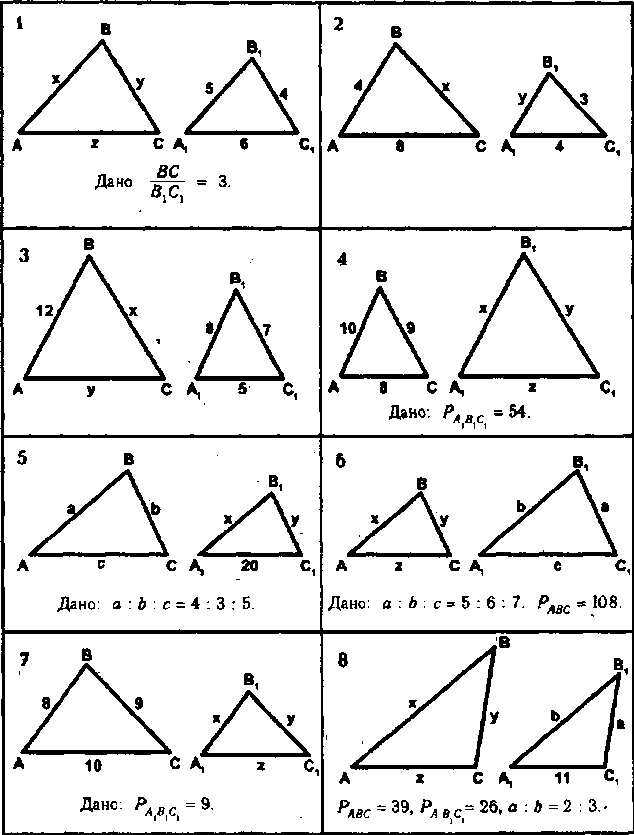
Таблица 9.1. Подобные треугольники

Дано: МВС <» ДЛ.В.С,. Найти х, у, г:

 

 

 

1)  Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ражённого на ри­сун­ке.

Решение:

Высота BH треугольника ABC нам дана: BH=24. Эта высота проведена к стороне AC.

AC=AH+HC=10+32=42.

Площадь треугольника ABC:  S_АВС=12AC⋅BH=12⋅42⋅24=21⋅24=504.

Ответ: S_АВС=504

2)  В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, а угол, ле­жа­щий на­про­тив него, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

Решение:

Пусть катет AC=10, лежащий напротив него ∠ABC=45∘. 

Как мы помним, если в прямоугольном треугольнике острый угол равен 45∘, то этот треугольник - равнобедренный: ΔABC - равнобедренный ⟹AC=BC=10.

Площадь прямоугольного треугольника -  полупроизведение его катетов: S_АВС=12⋅AC⋅BC=10⋅102=50.

Ответ: S=50

3) Найдите площадь треугольника, изображенного на рисунке.

Ответ 10

 

4) В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, ост­рый угол, при­ле­жа­щий к нему, равен 60°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на√. 3

Ответ 50

5) В пря­мо­уголь­ном тре­уголь­ни­ке ги­по­те­ну­за равна 70, а один из ост­рых углов равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

Ответ 1225

 

6) В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 120°. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на √3

Ответ 25

 

7) Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 216, а бо­ко­вая сто­ро­на — 78. Най­ди­те пло­щадь тре­уголь­ни­ка.

Ответ 2160

8) Вы­со­та рав­но­сто­рон­не­го тре­уголь­ни­ка равна 10. Най­ди­те его пло щадь, умноженную на√3.

Ответ 100

 

9) В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 8, ос­но­ва­ние — 5⋅(√6−√2), а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 30°. Най­ди­те пло­щадь тре­уголь­ни­ка.

Ответ 16

10) Дан выпуклый четырехугольник, углы которого относятся как 7:3:2:6. Найдите наибольший угол этого четырехугольника.

Ответ 140

 11) Найдите, чему равны стороны параллелограмма, если его периметр P=60, а стороны относятся как 1:2.

Решение:

Так как стороны относятся как 1:2, обозначим одну из сторон параллелограмма AB за 1x, тогда сторону BC - за 2x.

По свойству параллелограмма, противоположные стороны равны, т.е. CD=AB,  AD=BC.

Периметр параллелограмма - это сумма длин всех его четырех сторон:P=AB+BC+CD+AD=2⋅AB+2⋅BC⟹P=2⋅x+2⋅2x=6x.   P=6x⟹60=6x⟹x=10. Значит, стороны параллелограмма: AB=CD=x=10,   AD=BC=2x=20.

Ответ: 10,  20

12)  Разность двух углов, прилежащих к одной стороне параллелограмма, равна 40∘. Найти меньший угол параллелограмма.

Решение:

Обозначим ∠A  параллелограмма ABCD  за x. По условию задачи .

∠B−∠A=40∘⟹∠B=∠A+40∘⟹∠B=x+40∘.

Мы знаем, что сумма углов, прилежащих к одной стороне параллелограмма, равна 180∘.

∠A+∠B=180∘⟹x+x+40∘=180∘⟹2x=140∘⟹x=70∘.

Значит, ∠A=x=70∘,  ∠B=x+40∘=110∘. 

Меньший угол параллелограмма - это ∠A, его и записываем в ответ.

Ответ: 70∘

13) Диа­го­наль BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 65° и 50°. Най­ди­те мень­ший угол па­рал­ле­ло­грам­ма.

Решение:

Найдем сначала весь угол B: ∠B=∠ABD+∠DBC=65∘+50∘=115∘.

Сумма углов, прилежащих к одной стороне параллелограмма, равна 180∘: ∠A+∠B=180∘⟹∠A+115∘=180∘⟹∠A=180∘−115∘=65∘.

Нужно было найти меньший угол параллелограмма, это и есть угол A.

Ответ: 65∘
 

14) На про­дол­же­нии сто­ро­ны AD  па­рал­ле­ло­грам­ма ABCD  за точ­кой D от­ме­че­на точка E  так, что DC=DE. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD, если ∠DEC=53°. 

Решение:

Обратим сразу внимание, что ΔCDE  - равнобедренный с основанием CE. В равнобедренном треугольнике углы при основании равны: ∠DCE=∠DEC=53∘.

 ∠ADC - внешний угол треугольника CDE  при вершине D⟹∠ADC=∠DCE+∠DEC=53∘+53∘=106∘   

(внешний угол треугольника равен сумме двух углов, не смежных с ним). Мы нашли нужный нам больший угол параллелограмма. Меньший угол параллелограмма ∠A=180∘−∠D=180∘−106∘=74∘.

Ответ: 106∘

15) Най­ди­те ве­ли­чи­ну остро­го угла па­рал­ле­ло­грам­ма ABCD, если бис­сек­три­са угла A об­ра­зу­ет со сто­ро­ной BC угол, рав­ный 15°.

Решение:

Так как AL - биссектриса, то ∠BAL=∠LAD.

Из определения параллелограмма: BC||AD⟹∠BLA=∠LAD (как накрест лежащие углы при BC||AD и секущейAL).

Итак, ∠BAL=∠LAD=∠BLA=15∘.

Так как  ∠BAL=∠BLA⟹ΔABL - равнобедренный с основанием AL⟹AB=BL. Для решения данной задачи эта строчка не понадобится, но пригодится для решения одной из тестовых задач в этом уроке ;) 

∠BAD=∠BAL+∠LAD=15∘+15∘=30∘. Это и есть требуемый острый угол параллелограмма.

Ответ: 30∘ 

16) В па­рал­ле­ло­грам­ме ABCD диа­го­наль AC в 2 раза боль­ше сто­ро­ны AB и  ∠ACD=104°. Най­ди­те угол между диа­го­на­ля­ми па­рал­ле­ло­грам­ма. 

Решение:

Противоположные стороны параллелограмма равны ⟹CD=AB.

Обозначим сторону CD  за x, тогда диагональ AC=2x. По свойству параллелограмма диагонали AC  и BD  точкой пересечения O  делятся пополам, т.е. AO=OC=12AC=x.

В треугольнике COD  стороны CO  и  CD  оказались равны ⟹ΔCOD  - равнобедренный с основанием OD⟹∠COD=∠CDO  (как углы при основании равнобедренного треугольника).