Задачи с практическим содержанием

Задача по теме «Площадь круга и длина окружности». 9 класс

Колодец цилиндрической формы, имеющий в диаметре 135 см. , а глубину 380 м. , надо выложить кирпичом. Сколько штук кирпича для этого потребуется, если размер кирпича 25 х 12 х 6,5 см.

Решение:  Длина окружности, диаметр которой меньше диаметра колодца на удвоенную ширину кирпича, равна πd ≈ 351 см . Длину окружности делим на длину кирпича, получаем 351 : 25 ≈ 14 кирпичей уложено в один ряд. Таких рядов будет 380 : 6,5 ≈ 59. Следовательно, потребуется кирпича 14 ∙ 59 = 826 штук.

Ответ: 826 кирпичей.

Задача:  Поверхность пруда имеет форму квадрата.

В вершинах квадрата на берегу пруда растут четыре дуба. Хотят вдвое увеличить площадь повер- хности пруда, но так, чтобы новый пруд со- хранил форму квадрата и чтобы все четыре дуба остались целы (то есть были на берегу).  Как это сделать?

Решение: Построим точки О₁, О₂, О₃, О₄, симметричные точке О относительно прямых ВС, АD, CD, и АВ соответственно. Докажем, что Sо₁о₂ о₃ о₄ =2S_АВСD.  Пусть ВС = х. Тогда площадь пруда равна х2. Площадь нового пруда  Sо₁о₂ о₃ о₄ = О₁О₂ ∙ О₃О₄ = 2 х2.

Задача  по теме «Теоремы синусов и косинусов».

С наблюдательного пункта А замечают под углом 63°30( самолет В, пролетающий над башней D, высота которой 79,5 м. Прямая, соединяющая наблюдательный пункт А с верхушкой башни D, образует с горизонтальной плоскостью угол 20°45(. На какой высоте находился самолет?

Решение: Высота полета самолета ВС = ВD + DС ∆ ABC – прямоугольный, т. к. СВ – высота. (DAB =(САВ – (САD = 63°30( – 20°45( = 42°45(, (СВА=90° – 63°30) = 26°30 (.∆ DАС – прямоугольный. АD =Из ∆ DAB по теореме синусов ВС = ВD + DС = 342,2 + 79,5 = 421,7

Ответ: 421,7 м – высота полета самолета.

Задача  по теме «Теоремы синусов и косинусов».

Вершина горы В (рис. 10) из точки А видна под углом  = 38°42 а при приближении к горе на 200 м вершина стала видна под углом = 42°).  Найти высоту горы.

Решение:  Из ∆ BDC по теореме синусов ∆ BDC – прямоугольный, т. к. ВС - высота горы.

Ответ: высота горы 1452,5 м.

Дерево имеет в обхвате 120 см. Найдите примерную площадь поперечного сечения (в см²), имеющего форму круга. (П=3)

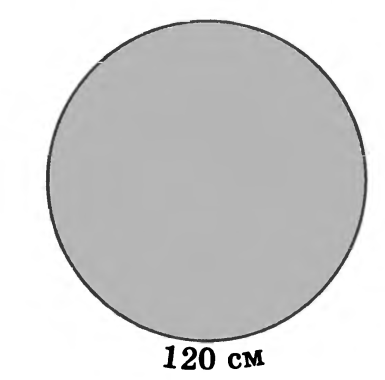
Ответ:1200

Две трубы, диаметры которых равны 10 см и 24 см, требуются заменить одной, не изменяя их пропускной способности. Каким должен быть диаметр новой трубы?

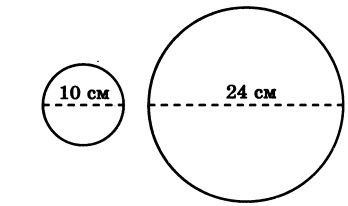
Ответ:26

Зрачок человеческого глаза, имеющий форму круга, может изменять свой диаметр в зависимости от освещения от 1,5 мм до 7,5 мм. Во сколько раз при этом увеличивается площадь поверхности зрачка?

Ответ:25

Бумажная лента плотно намотана на катушку, внутренний диаметр которой равен 20 см. Толщина бумаги равна 0,5 мм, а толщина намотанного рулона – 30 см. Найдите длину бумажной ленты. Ответ дайте в метрах (П=3)

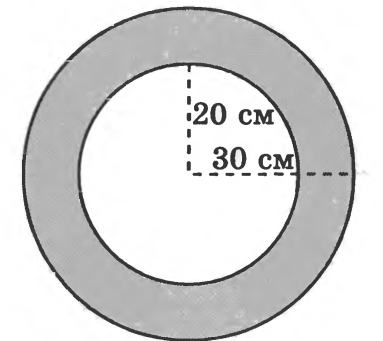
Ответ:300

Участок между двумя параллельными улицами имеет вид четырехугольника ABCD (AD\\BC)  AB=28м, ВС=20м, AD=40м, угол В=112⁰. Найдите площадь этого участка. В ответе укажите приближенное значение, равное целому числу квадратных метров.

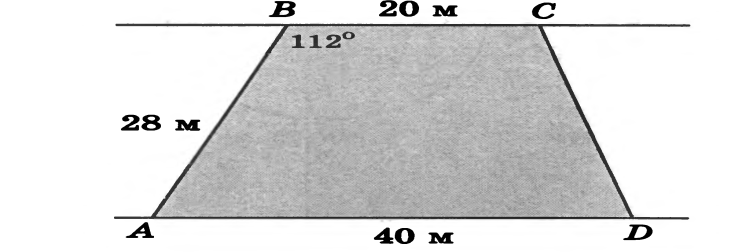
Ответ:1875

«Тригонометрические функции. Решение треугольников »

1 вариант

1. Мальчик прошел от дома по направлению на восток 800м. Затем завернул на север и прошел 600м. Под каким углом к направлению на запад он должен идти, чтобы вернуться домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций)

Ответ 37

2. Горная железная дорога поднимается на 1 м на каждые 30м пути. Используя таблицу тригонометрических функций, найдите угол подъема в градусах. В ответе укажите приближенное значение, выраженное целым числом.

Ответ  2        

3. Лестница имеет ступеньки, ширина которых30 см, а высота – 18 см. Используя таблицу тригонометрических функций, найдите угол подъема лестницы. В ответе укажите приближенное значение, выраженное целым числом.

Ответ 31       

4. С самолета радируют капитану рыболовецкого судна, что самолет находится над косяком рыбы на высоте 1000 м. С судна определяют, что угол, под которым виден самолет над горизонтом, равен 26⁰. Используя таблицу тригонометрических функций, найдите расстояние от судна до косяка рыбы. В ответе укажите приближенное значение, выраженное целым числом.

Ответ 2020   

Использую данные, приведенные на рисунке, найдите ширину АВ реки.

Ответ 23,8

 «Тригонометрические функции. Решение треугольников »

2. вариант

1. Девочка прошла от дома на запад 500 м. Затем повернула на север и прошла 300м. После этого она повернула на восток и прошла еще 100 м. Под каким углом к направлению на восток она должна идти, чтобы вернуться домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций)

Ответ  37

2. Человек, пройдя вверх по склону холма на 1000 м, поднялся на 90 м над плоскостью основания холма. Используйте таблицу тригонометрических функций, найдите (в среднем) угол наклона холма в градусах. В ответе укажите приближенное значение, выраженное целым числом.

Ответ       5         

3. Угол подъема лестница дачного домика равен 58⁰. Используйте таблицу тригонометрических функций, найдите высоту ступенек лестницы, если ширина ступенек равна 20 см.

Ответ 32 

4. Самолет приближается к аэропорту А на высоте 8000м. Пилот имеет предписание производить снижение для посадки под постоянным углом 6⁰. Используйте таблицу тригонометрических функций, найдите расстояние АВ от посадочной полосы до того места, над которым самолет должен начать снижение. В ответе укажите приближенное значение, выраженное целым числом метров.

Ответ 76080 

5. Из окна, расположенного на высоте 15 м над поверхностью земли, нижний край дома, стоящего прямо на другой стороне улицы, виден под углом понижения 32⁰. Найдите ширину улицы.

Ответ 24