ЕГЭ 11 класс
Этот раздел содержит типовые задачи входящие в единый государственный экзамен, а также содержит ряд тренировочных экзаменационных задач в части Геометрии для подготовки экзамену.
- Справочный материал для базового ЕГЭ
Для проверки решения отправьте ответ 
Задание № 3 — является заданием базового уровня первой части, проверяет умения выполнять действия с геометрическими фигурами по содержанию курса «Планиметрия». В задании 3 проверяется умение вычислять площадь фигуры на клетчатой бумаге, умение вычислять градусные меры углов, вычислять периметры и т.п.
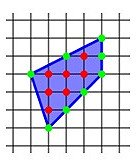
Пример 3. Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Посмотреть решение (при нажатии выводится решение)
Решение: Для вычисления площади данной фигуры можно воспользоваться формулой Пика:
|
На рисунке справа B = 7 (красные точки), Г = 8 (зелёные точки),
Для вычисления площади данного прямоугольника воспользуемся формулой Пика:
где В = 10, Г = 6, поэтому
Ответ: 20. |
||||||||||||||||
Задание № 6 по планиметрии на нахождение геометрических величин (длин, углов, площадей), моделирование реальных ситуаций на языке геометрии. Исследование построенных моделей с использованием геометрических понятий и теорем. Источником трудностей является, как правило, незнание или неверное применение необходимых теорем планиметрии.
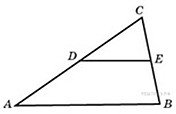
Пример 6. Площадь треугольника ABC равна 129. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Посмотреть решение (при нажатии выводится решение)
Решение. Треугольник CDE подобен треугольнику CAB по двум углам, так как угол при вершине C общий, угол СDE равен углу CAB как соответственные углы при DE || AB секущей AC. Так как DE – средняя линия треугольника по условию, то по свойству средней линии | DE = (1/2)AB. Значит, коэффициент подобия равен 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
|
SΔCDE |
= |
|
2 |
|
2 |
; SΔCDE = |
1 |
· 129 = 32,25. |
|
SΔCAB |
5 |
|
4 |
Следовательно, SABED = SΔABC – SΔCDE = 129 – 32,25 = 96,75.
Ответ: 96,75.
Задание № 8 — проверяет у участников экзамена знания по элементарной стереометрии, умение применять формулы нахождения площадей поверхностей и объемов фигур, двугранных углов, сравнивать объемы подобных фигур, уметь выполнять действия с геометрическими фигурами, координатами и векторами и т.п.
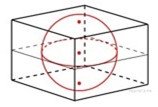
Пример 8. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
Посмотреть решение (при нажатии выводится решение)
Решение. 1) Vкуба = a3 (где а – длина ребра куба), поэтому
а3 = 216
а = 3√216
a = 6.
2) Так как сфера вписана в куб, значит, длина диаметра сферы равна длине ребра куба, поэтому d = a, d = 6, d = 2R, R = 6 : 2 = 3.
Ответ: 3.
Задание № 14 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
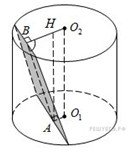
Пример 14. Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между хордами равно 2√197.
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Посмотреть решение (при нажатии выводится решение)
Решение: а) Хорда длиной 12 находится на расстоянии 
= 8 от центра окружности основания, а хорда длиной 16, аналогично, – на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14, либо 8 − 6 = 2.
Тогда расстояние между хордами составляет либо
= 
= √980 = 
= 2√245
либо
= 
= √788 = 
= 2√197.
По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее. Что требовалось доказать.
б) Обозначим центры оснований за О1 и О2. Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости β, перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание — H (H ∈ β). Тогда AB,AH ∈ β и значит, AB,AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.
Значит, искомый угол равен
|
∠ABH = arctg |
AH |
= arctg |
28 |
= arctg14. |
|
BH |
8 – 6 |
Ответ: arctg 14.
Задание № 16 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами, координатами и векторами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
Пример 16. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E – на отрезке AB. а) Докажите, что FH = 2DH. б) Найдите площадь прямоугольника DEFH, если AB = 4.
Посмотреть решение (при нажатии выводится решение)
Решение: а)
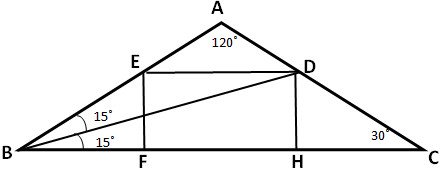
1) ΔBEF – прямоугольный, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тогда EF = 
BE по свойству катета, лежащего против угла 30°.
2) Пусть EF = DH = x, тогда BE = 2x, BF = x√3 по теореме Пифагора.
3) Так как ΔABC равнобедренный, значит, ∠B = ∠C = 30˚.
BD – биссектриса ∠B, значит ∠ABD = ∠DBC = 15˚.
4) Рассмотрим ΔDBH – прямоугольный, т.к. DH⊥BC.
|
tg ∠DBH = |
DH |
|
BH |
|
tg 15° = tg(45° – 30°) = |
3 – √3 |
, |
|
3 + √3 |
|
3 – √3 |
, |
x |
|
3 + √3 |
x√3 + FH |
(x√3 + FH)(3 – √3) = x(3 + √3)
2√3x – 6x = √3FH – 3FH
2x(√3 – 3) = FH(√3 – 3)
FH = 2x
FH = 2DH
Что требовалось доказать.
б) 1) ΔAED ∼ ΔABC по двум углам, так как ∠B – общий, ∠AED = ∠ABC как соответственные при ED || BC секущей AB. Из подобия треугольников следует:
|
ED |
= |
AE |
|
BC |
AB |
|
2x |
= |
4 – 2x |
|
2x(√3 + 1) |
4 |
|
1 |
= |
2 – x |
|
√3 + 1 |
2 |
√3 – 1 = 2 – x
x = 3 – √3
EF = 3 – √3
2) SDEFH = ED · EF = (3 – √3) · 2(3 – √3)
SDEFH = 24 – 12√3.
Ответ: 24 – 12√3.
https://www.metod-kopilka.ru/podborka_zadach_dlya_podgotovki_k_ege_po_geometrii-47221.htm
Набор заданий.
1 вариант (при нажатии появляются задания)
1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
2. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
3. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
4. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
5. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
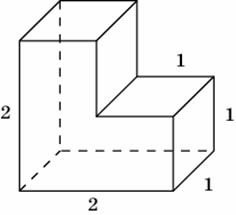
6. Из единичного куба выр